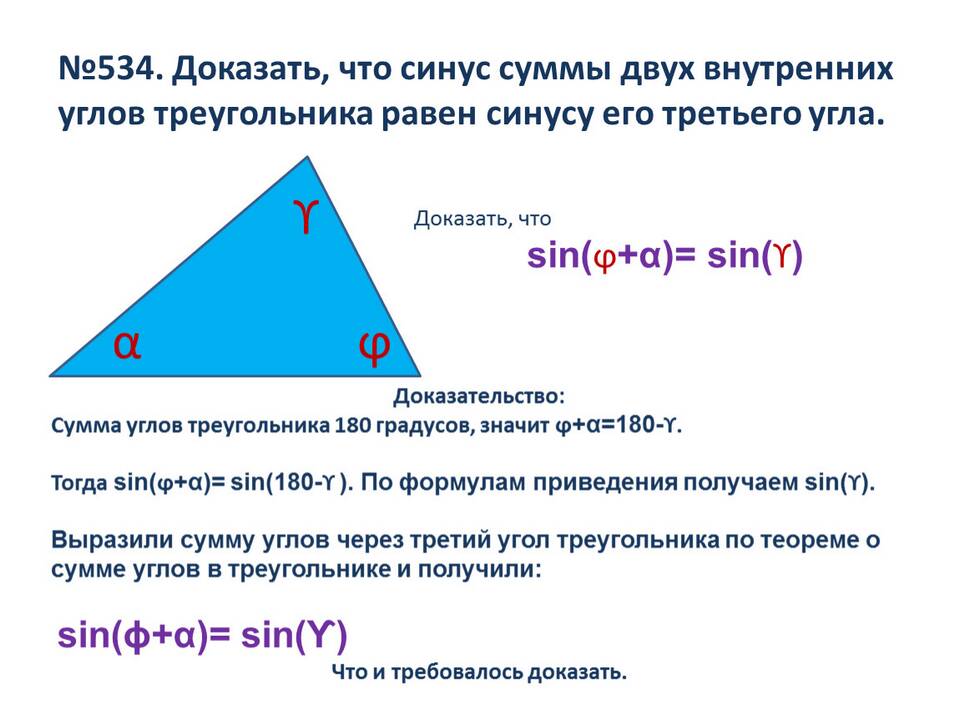
Тангенс суммы двух углов - это тригонометрическая функция, выражающаяся через тангенсы отдельных углов. Данная формула широко применяется в математике, физике и инженерных расчетах.
Содержание
Формула тангенса суммы
Основная формула для тангенса суммы двух углов α и β выглядит следующим образом:
| tan(α + β) = | (tanα + tanβ) / (1 - tanα·tanβ) |
Вывод формулы
Формула выводится из тригонометрических тождеств для синуса и косинуса суммы углов:
- sin(α + β) = sinα·cosβ + cosα·sinβ
- cos(α + β) = cosα·cosβ - sinα·sinβ
- tan(α + β) = sin(α + β)/cos(α + β)
- После подстановки и деления на cosα·cosβ получаем конечную формулу
Особые случаи
| Условие | Результат |
| α = β | tan(2α) = 2tanα/(1 - tan²α) - формула двойного угла |
| α + β = 90° | tan(α + β) не существует (бесконечность) |
| α или β = 0 | tan(α + 0) = tanα |
Примеры применения
- Вычисление точных значений тригонометрических функций
- Решение тригонометрических уравнений
- Доказательство других тригонометрических тождеств
- Приложения в физике (оптика, механика)
Пример расчета
Найти tan(45° + 30°):
| tan45° = 1 | tan30° = √3/3 |
| tan(75°) = (1 + √3/3)/(1 - 1·√3/3) = (3 + √3)/(3 - √3) | |
Графическая интерпретация
На единичной окружности тангенс суммы углов соответствует отношению суммы координат y к сумме координат x для комбинации двух углов.
Ограничения формулы
- Формула не работает при α + β = 90° + 180°n (n ∈ ℤ)
- Требует знания точных значений tanα и tanβ
- При больших углах может приводить к потере точности вычислений
Дополнительные формулы
Аналогичным образом можно получить формулу для тангенса разности углов:
| tan(α - β) = | (tanα - tanβ) / (1 + tanα·tanβ) |